问题
解答题
某车间将10名技工平均分成甲、乙两组加工某种零件，在单位时间内每个技工加工的合格零件数如下表：
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工，对其加工的零件进行检测，若2人加工的合格零件个数之和超过14，则称该车间“质量合格”，求该车间“质量合格”的概率． |
答案
（1）两组技工水平基本相当，乙组更稳定些（2）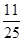
(1)由甲组技工在单位时间内加工的合格零件平均数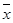
甲＝
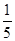(4＋5＋x＋9＋10)＝7，得x＝7.
由乙组技工在单位时间内加工的合格零件平均数
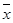乙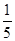＝(5＋6＋7＋y＋9)＝7，得y＝8.
甲组方差
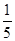＝[(4－7)2＋(5－7)2＋(7－7)2＋(9－7)2＋(10－7)2]＝5.2.
乙组方差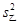
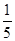＝[(5－7)2＋(6－7)2＋(7－7)2＋(8－7)2＋(9－7)2]＝2.
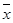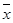∵甲＝乙， > ，
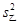∴两组技工水平基本相当，乙组更稳定些．
(2)从甲、乙两组中各随机抽取一名技工，加工的合格零件个数包含的基本事件为(4,5)，(4,6)，(4,7)，(4,8)，(4,9)，(5,5)，(5,6)，(5,7)，(5,8)，(5,9)，(7,5)，(7,6)，(7,7)，(7,8)，(7,9)，(9,5)，(9,6)，(9,7)，(9,8)，(9,9)，(10,5)，(10,6)，(10,7)，(10,8)，(10,9)，共25个．
而车间“质量合格”包含的基本事件为(7,8)，(7,9)，(9,6)，(9,7)，(9,8)，(9,9)，(10,5)，(10,6)，(10,7)，(10,8)，(10,9)，共11个，
因此，所求概率P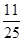＝，即该车间“质量合格”的概率为.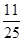