如图所示,总质量为m=75kg的滑雪者以初速度v0=8m/s沿倾角为θ=37°的斜面向上自由滑行,已知雪橇与斜面问动摩擦因数μ=0.25,假设斜面足够长.不计空气阻力.试求:
(1)滑雪者沿斜面上滑的最大距离.
(2)若滑雪者滑至最高点后掉转方向向下自由滑行,求他滑到起点时的速度大小.

(1)上滑过程中对人进行受力分析,滑雪者受重力mg,弹力FN,摩擦力f,并设滑雪者的加速度为a1,受力如图
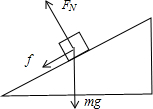
根据牛顿第二定律有:
mgsinθ+f=ma1,a1 的方向沿斜面向下. ①
由平衡关系有:FN=mgcosθ ②
根据动摩擦定律有:f=μFN ③
由以上各式解得:a1=g(sinθ+μcosθ)=8m/s ④
滑雪者沿斜面向上做匀减速直线运动,减速到零的位移为:x=
=4m ⑤v02 2a1
即滑雪者上滑的最大距离为4m
(2)滑雪者沿斜面下滑时,滑雪者收到的摩擦力沿斜面向上,受力如图
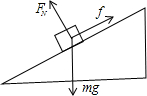
设加速度大小为a2
根据牛顿第二定律有:
mgsinθ-f=ma2 ⑥
由平衡关系有:FN=mgcosθ ⑦
根据动摩擦定律有:f=μFN ⑧
由以上各式解得:a2=g(sinθ-μcosθ)=4m/s2 ⑨
滑雪者沿斜面向下做初速度为零的匀加速直线运动,滑到出发点的位移为:x=4m/s
则滑雪者再次回到起点的速度为:v=
=42a2x
m/s=5.7m/s ⑩2
答:(1)滑雪者沿斜面上滑的最大距离4m
(2)滑雪者再次回到起点的速度为5.7m/s
