问题
解答题
已知数列{an}是各项均不为0的等差数列，公差为d，Sn为其前n项和，且满足
（1）求a1、d和Tn； （2）是否存在实数λ，使对任意的n∈N*，不等式λTn＜n+8恒成立？若存在，请求出实数λ的取值范围；若不存在，请说明理由． |
答案
（1）由题意可得，
=S1=a1，a 21
∵a1≠0，
∴a1=1．…．（1分）
∵
=S3=a1+a2+a3，a 22
∴（1+d）2=3+3d，
∴d=-1，2，当d=-1时，a2=0不满足条件，舍去．
因此d=2．…．（4分）
∴an=2n-1，
∴bn=
-1 2n-1
，1 2n+1
∴Tn=1-
+1 3
-1 3
+…+1 5
-1 2n-1 1 2n+1
∴Tn=1-
=1 2n+1
．…．（6分）2n 2n+1
（2）由题意可得，λ•
＜n+8，2n 2n+1
∴λ＜
=(2n+1)(n+8) 2n
(2n+1 2
+17)，…．（8分）8 n
∵2n+
≥8，当n=2时等号成立，…．（10分）8 n
∴
(2n+1 2
+17)最小值为8 n
，…．（12分）25 2
因此λ＜
． …．（14分）25 2
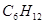，分子结构中含有3个“—
”原子团的烯烃共有 （ ）