问题
选择题
若数列{an}的前n项和Sn=n2(n∈N*),则
|
答案
当n=1时,a1=s1=1
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1
总之an=2n-1
∴
=1 anan+1
=1 (2n-1)(2n+1)
(1 2
-1 2n-1
)1 2n+1
∴
+1 a1a2
+…+1 a2a3 1 anan+1
=
(1-1 2
+1 3
-1 3
+1 5
-1 5
+…+1 7
-1 2n-1
)1 2n+1
=
(1-1 2
)1 2n+1
=n 2n+1
故选A

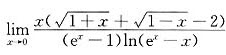 =()。
=()。