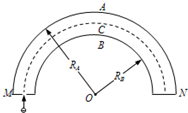
“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.
(1)判断球面A、B的电势高低,并说明理由;
(2)求等势面C所在处电场强度E的大小;
(3)若半球面A、B和等势面C的电势分别为φA、φB和φC,则到达N板左、右边缘处的电子,经过偏转电场前、后的动能改变量△Ek左和△Ek右分别为多少?
(4)比较|△Ek左|和|△Ek右|的大小,并说明理由.
(1)电子做匀速圆周运动,电场力提供向心力,受力的方向与电场的方向相反,所以B板的电势较高;
(2)电场力提供向心力:eE=mv2 R
又:R=
,EK0=RA+RB 2
mv21 2
联立以上3式,得:E=4Ek0 e(RA+RB)
(3)到达N板左、右边缘处的电子,在运动的过程中,电场力对它们做功,电子动能的改变量等于电场力做功,即:
△EK左=eUCB=e(φC-φB),△EK右=eUCA=e(φC-φA)
(4)该电场是放射状电场,内侧的电场线密,电场强度大,所以UBC>UCA,即:φC-φB>φC-φA,所以:|△EK左|>|△EK右|
答:(1)B板电势高于A板; (2)求等势面C所在处电场强度E的大小E=
;(3)△Ek左=e(φC-φB),△Ek右=e(φC-φA);(4)|△Ek左|>|△Ek右|4Ek0 e(RA+RB)
