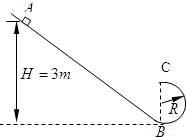
如图所示,粗糙的斜槽轨道与半径R=0.5m的光滑半圆形轨道BC连接,B为半圆轨道的最底点,C为最高点.一个质量m=0.5kg的带电体,从高为H=3m的A处由静止开始滑下,当滑到B处时速度υB=4m/s,此时在整个空间加上一个与纸面平行的匀强电场,带电体所受电场力在竖直向上的分力大小与重力相等.带电体沿着圆形轨道运动,脱离C处后运动的加速度是υym/s2,经过一段时间后运动到斜槽轨道某处时速度的大小是υ=2m/s.已知重力加速度g=10m/s2,带电体运动过程中电量不变,经过B点时能量损失不计,忽略空气的阻力.求:
(1)带电体从B到C的过程中电场力所做的功W
(2)带电体运动到C时对轨道的压力F
(3)带电体与斜槽轨道之间的动摩擦因数μ
解;(1)设带电体受到电场力的水平分量为Fx,竖直分量为Fy,带电体由B到C的运动过程中,水平分力做功为零,竖直分力做功等于重力做功.
即:W=Fy•2R=mg•2R=5J
(2)带电体从B到C运动的过程中,重力和电场力的竖直分力相等,电场力的水平分力不做功,所以υC=υB=4m/s
在C点,由牛顿第二定律得:F+mg-Fy=mυ2 R
又mg=Fy解得:F=16N
(3)带电体脱离轨道后在水平方向上做匀减速直线运动,由运动学公式得:
υC2-υ2=2ax
代入数据得:x=
m3
设斜面与水平面的夹角为α,则tanα=
=2R x
,α=30°3 3
带电体从A到B的运动过程中,由动能定理的:mgH-μmgcosα
=H sinα
mυB21 2
代入数据解得:μ=11 3 45
答:
(1)带电体从B到C的过程中电场力所做的功W=5J.
(2)带电体运动到C时对轨道的压力F=16N.
(3)带电体与斜槽轨道之间的动摩擦因数μ=
.11 3 45

