问题
问答题
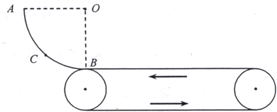
如图所示,固定的光滑圆弧轨道ACB的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m.物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2.若物块从A点下滑到传送带上后,又恰能返回到C点,
(1)求传送带的速度.
(2)求物块在传送带上第一次往返所用的时间.
答案
由机械能守恒定律得mgr=
m1 2
,v 2B
VB=
=4m/s;2gr
物块先在传送带上作匀减速直线运动,运动时间为t1=
=0-VB a
=4s,0-4 -1
通过的位移为x1=
=0 -V 2B 2a
=8m;02-42 -2×1
物块再在传送带上作匀加速直线运动,其末速度由mgh=
m1 2 v 21
得v1=
=2m/s,2gh
则匀加速直线运动的时间为t2=
=v1-0 a
=2s,0-2 1
通过的位移为x2=
=v 21 2a
=2m,22 2×1
然后再作匀速运动,故传送带的速度应为2m/s;
其位移为通过的位移为x3=x1-x2=8-2=6m,匀速运动的时间为t3=
=x3 v1
=3s,6 2
所以物块在传送带上第一次往返所用的时间为t=t1+t2+t3=4+2+3=9s.
答:(1)传送带的速度为2m/s;(2)物体第一次往返的时间为9s.
