问题
解答题
已知f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定义域；
(2)在函数图象上是否存在不同两点，使过两点的直线平行于x轴?
答案
(1)由ax-bx>0，得(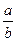
)x>1=(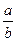)0.
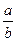∵>1，∴x>0.
∴函数的定义域为(0，+∞).
(2)先证明f(x)是增函数.
对于任意x1>x2>0，∵a>1>b>0，
∴
>
，
<
.
∴->-.
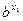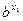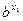∴lg(-)>lg(-).
∴f(x1)>f(x2).
∴f(x)在(0，+∞)上为增函数.
假设y=f(x)上存在不同的两点A(x1，y1)、B(x2，y2)，使直线AB平行于x轴，
则x1≠x2，y1=y2，这与f(x)是增函数矛盾.
∴y=f(x)的图象上不存在两点，使过这两点的直线平行于x轴.
(2)的思维难点是把问题化归为研究函数的单调性问题.