如图所示，半径R=0.1m的竖直半圆形光滑轨道bc与水平面ab相切．质

问题问答题

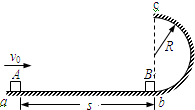
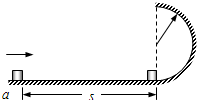
如图所示，半径R=0.1m的竖直半圆形光滑轨道bc与水平面ab相切．质量m=0.1kg的小滑块B放在半圆形轨道末端的b点，另一质量也为m=0.1kg的小滑块A以v₀=2

m/s的水平初速度向B滑行，滑过s=1m的距离，与B相碰，碰撞时间极短，碰后A、B粘在一起运动．已知木块A与水平面之间的动摩擦因数μ=0.2．A、B均可视为质点．（g=10m/s²）．求：

（1）A与B碰撞前瞬间的速度大小v_A；

（2）碰后瞬间，A、B共同的速度大小v；

（3）在半圆形轨道的最高点c，轨道对A、B的作用力N的大小．

答案

（1）滑块做匀减速直线运动，加速度大小：a=

=2 m/s^{2
v_A²-v₀²=-2ax
解得：v_A=6m/s
答：A与B碰撞前瞬间的速度大小为6m/s．
（2）碰撞过程中满足动量守恒：mv_A=2mv
解得：v=3m/s
答：碰后瞬间，A与B共同的速度大小为3m/s．
（3）由b运动到a的过程中，根据动能定理
设a点的速度为v_c，
-4mgr=mv²-mv_c²
解得：v_c=
5
m/s
根据受力分析：mg+N=m
v2
r
解得：N=8N
答：轨道对A与B的作用力N的大小为8N．}