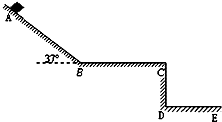
如图所示,质量m=6.0kg物块(可视为质点)从斜面上的A点由静止开始下滑,滑到斜面底端B后沿水平桌面再滑行一段距离后从C点飞出,最后落在水平面上的E点.已知物块与斜面、水平桌面间的动摩擦因数都为μ=0.50,斜坡的倾角θ=37°,CD高h=0.45m,BC长L=2.0m,DE长S=1.2m.假设斜坡与水平桌面间是平滑连接的,整个运动过程中空气阻力忽略不计.试求:
(1)物块经过C点的速度大小;
(2)物体在B点的速度大小;
(3)物体在斜面上滑行的时间.
(1)物块从C到E的过程做平抛运动
竖直方向做自由落体运动 h=
gt2 0.45=10×1 2
t2 解得t=0.3 s 1 2
水平方向做匀速直线运动 S=VCt 1.2=VC×0.3 得 VC=4m/s
即物块经过C点的速度大小为4m/s.
(2)物块从B到C的过程做匀减速运动,设加速度为a1
f1=-μmg=ma1 a1=-μg=-5m/s2
由 2a1L=VC2-VB2 2×(-5)×2=42-VB2得 VB=6m/s
即物体在B点的速度大小为6m/s.
(3)设物块在斜坡上时的加速度为a2,根据牛顿第二定律,有
mgsin37°-μmgcos37°=ma2 a2=2m/s2
斜面上匀加速运动VB=a2t t=3s
即物体在斜面上滑行的时间为3s.