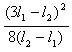问题
计算题
已知O、A、B、C为同一直线上的四点,AB间的距离为l1,BC间的距离为l2,一物体自O点由静止出发,沿此直线做匀加速运动,依次经过A、B、C三点,已知物体通过AB段与BC段所用的时间相等。求O与A的距离。
答案
解:设物体的加速度为a,到达A点的速度为v0,通过AB段和BC段所用的时间为t,则有
l1= v0t+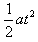
l1+l2= 2v0t+2at2
联立解得:l2-l1=at2 ,3l1-l2=2v0t
解得:a=4v02(l2-l1)/(3l1-l2)2
设O与A的距离为l,则有l =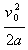 =
=