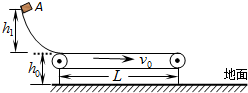
如图所示,一光滑的曲面与长L=2m的水平传送带左端平滑连接,一滑块从曲面上某位置由静止开始下滑,滑块与传送带间的动摩擦因数μ=0.5,传送带离地面高度h0=0.8m.
(1)若传送带固定不动,滑块从曲面上离传送带高度h1=1.8m的A处开始下滑,求滑块落地点与传送带右端的水平距离;
(2)若传送带以速率v0=5m/s顺时针匀速转动,求滑块在传送带上运动的时间.
(1)滑块滑至水平传送带的初速度为v1,则
mv12=mgh1,1 2
v1=
=6m/s2gh1
滑块的加速度a=μg,设滑块到达传送带右端的速度为v2,
由v22-v12=-2aL
得v2=4m/s.
滑块到达传送带右端做平抛运动,设平抛运动的时间为t,
则h0=
gt2t=1 2
=0.4s2h0 g
落地点与传送带右端的水平距离x=v2t=1.6m
(2)设滑块从传送带左端运动到和传送带速度v0相同时所用时间为t1,位移为x1,
由v0=v1-at1,得t1=0.2s
由x1=
t1=1.1m<Lv1+v0 2
说明滑块先做匀加速运动后做匀速运动,x2=L-x1=0.9m
滑块做匀速运动的时间t2=
=0.18sx2 v0
所以t总=t1+t2=0.38s
答:(1)滑块落地点与传送带右端的水平距离是1.6m;
(2)滑块在传送带上运动的时间是0.38s.