问题
解答题
已知函数f(x)=logax(a＞0,a≠1)，如果对于任意x∈［3，+∞）都有|f(x)|≥1成立，试求a的取值范围.
答案
a的取值范围是：(1，3］∪［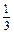
，1）
当a＞1时，对于任意x∈［3，+∞），都有f(x)＞0.
所以，|f(x)|=f(x),而f(x)=logax在［3，+∞）上为增函数，
∴对于任意x∈［3，+∞），有f(x)≥loga3. 4分
因此，要使|f(x)|≥1对于任意x∈［3，+∞）都成立.
只要loga3≥1=logaa即可，∴1＜a≤3. 6分
当0＜a＜1时，对于x∈［3，+∞），有f(x)＜0,
∴|f(x)|="-f(x). " 8分
∵f（x）=logax在［3，+∞）上为减函数，
∴-f（x）在［3，+∞）上为增函数.
∴对于任意x∈［3，+∞）都有
|f(x)|=-f(x)≥-loga3. 10分
因此，要使|f(x)|≥1对于任意x∈［3，+∞）都成立，
只要-loga3≥1成立即可，
∴loga3≤-1=loga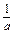
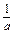,即≤3,∴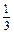≤a＜1. 12分
综上，使|f(x)|≥1对任意x∈［3，+∞）都成立的a的取值范围是：(1，3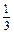］∪［，1）. 14分