问题
填空题
设f(n)=1+
|
答案
f(1)=1
f(2)=1+1 2
f(3)=1+
+1 2 1 3
…
f(n)=1+
+1 2
+…1 3 1 n
所以f(1)+f(2)+f(3)+…+f(n)
=n×1+
(n-1)+1 2
(n-2)…1 3
[n-(n-1)]1 n
=n[1+
+1 2
+…1 3
]-[1 n
+1 2
+2 3
…3 4
]n-1 n
=nf(n)-[1-
+1-1 2
+1-1 3
…1-1 4
]1 n
=nf(n)-[(n-1)-f(n)+1]
=(n+1)f(n)-n
因为f(1)+f(2)+f(3)+…+f(n)+n=ng(n)f(n)
所以(n+1)f(n)=ng(n)f(n)
所以g(n)=n+1 n
故答案为:存在,通项公式g(n)=n+1 n

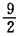 天可以完成全路的
天可以完成全路的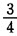 ,这条路长多少公里()
,这条路长多少公里()