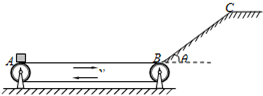
用图所示的水平传送带AB和斜面BC将货物运送到斜面的顶端.传送带AB的长度L=11m,上表面保持匀速向右运行,运行的速度v=12m/s.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔△t=1.0s将一个质量m=10kg的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的
,g=10m/s2(sin37°=0.6,cos37°=0.8).求:1 11
(1)斜面与货物箱之间的动摩擦因数μ;
(2)从第一个货物箱放上传送带A端开始计时,在t0=3.0s的时间内,所有货物箱与传送带的摩擦产生的热量Q;
(3)如果C点处的机器人操作失误,未能将第一个到达C点的货物箱搬走而造成与第二个货物箱在斜面上相撞.求两个货物箱在斜面上相撞的位置到C点的距离.(本问结果可以用根式表示)
(1)货物箱在传送带上做匀加速运动过程,根据牛顿第二定律有
μ0mg=ma0
解得:a0=μ0g=5.5m/s2
由运动学公式:v12=2a0L
解得货物箱运动到传送带右端时的速度大小为:v1=11m/s
货物箱刚冲上斜面时的速度 v2=(1-
)v1=10m/s1 11
货物箱在斜面上向上运动过程中v22=2a1s
解得:a1=10m/s2
根据牛顿第二定律:mgsinθ+μmgcosθ=ma1
解得:μ=0.5;
(2)3.0s内放上传送带的货物箱有3个,前2个已经通过传送带,它们在传送带上的加速时间t1=t2=2.0s;第3个还在传送带上运动,其加速时间 t3=1.0s.
前2个货物箱与传送带之间的相对位移
△s=vt1-
v1t1=13m1 2
第3个货物箱与传送带之间的相对位移
△s′=vt3-
v1t3=9.25m 1 4
前2个货物箱与传送带摩擦产生的总热量为:
Q1=2μ0 mg△s=1430J
第三个货物箱与传送带摩擦产生的热量为:
Q2=μ0 mg△s′=508.75J.
总共生热 Q=Q1+Q2=1938.75J.
(3)货物箱由A运动到B的时间为2.0s,由B运动到C的时间为1.0s,可见第一个货物箱冲上斜面C端时第二个货物箱刚好冲上斜面.
货物箱沿斜面向下运动,根据牛顿第二定律有
mgsinθ-μmgcosθ=ma2
解得加速度大小a2=2.0m/s2
设第一个货物箱在斜面C端沿斜面向下运动与第二个货物箱相撞的过程所用时间为t,
有:v2t-
a1t 2+1 2
a2t 2=s1 2
解得:t=
s≈0.69 s 5- 5 4
两个货物箱在斜面上相遇的位置到C端的距离
s1=
a2t2=1 2
m≈0.48 m 30-10 5 16
答:(1)斜面与货物箱之间的动摩擦因数μ为0.5;
(2)从第一个货物箱放上传送带A端开始计时,在t0=3.0s的时间内,所有货物箱与传送带的摩擦产生的热量Q为1938.75J;
(3)两个货物箱在斜面上相撞的位置到C点的距离为0.48 m.