问题
解答题
设同时满足条件:①
(Ⅰ)若数列{an} 为等差数列,Sn是其前n项和,a3=4,S3=18,求Sn; (Ⅱ)判断(Ⅰ)中的数列{Sn}是否为“特界”数列,并说明理由. |
答案
(Ⅰ)设等差数列{an}的公差为,
a1+2d=4,3a1+3d=18,…(2分)
解得a1=8,d=-2…(4分)
Sn=na1+
d=-n2+9n…(6分)n(n-1) 2
(Ⅱ)由
-Sn+1=Sn+ SN+2 2
=(Sn+2-Sn+1)-(Sn+1- Sn) 2
=an+1- an+1 2
=-1<0d 2
得
<Sn+1,Sn+Sn+2 2
故数列数列{Sn}适合条件①…(9分)
Sn=-n2+9n=-(n-
)2+9 2
,81 4
则当n=4或n=5时,Sn有最大值20
即Sn≤20,故数列{Sn}适合条件②.
综上,故数列{Sn}是“特界”数列.…(12分)

 A
A /2
/2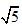 /2A
/2A