问题
解答题
已知一抛物线过点O（0，0），A（6，0），B（4，3）
（1）求这个抛物线的解析式；
（2）若P为抛物线在第一象限的一点，求△POA面积的最大值；
（3）抛物线的对称轴与直线OB交于点M，点C的坐标是（0，3），点Q为抛物线的对称轴上的一动点，以Q、O、M为顶点的三角形与△OBC相似，求出符合条件的Q点的坐标。
答案
解：（1）设该抛物线的解析式为
由已知，抛物线过（0，0）、（6，0），（4，3）三点，得
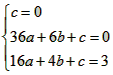
解得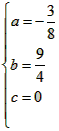
所求抛物线的解析式为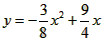
（2）∵△POA的底边OA=6，
∴当S△POA有最大值时，点P须位于抛物线的最高点，
∵
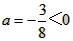，∴抛物线的顶点为最高点，
∴顶点坐标为（3，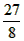
）
∴S△POA的最大值=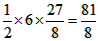
（3）抛物线的对称轴与x轴的交点Q1符合条件，
∵CB∥OA，
∴∠Q1OM=∠B，
∵∠BCO=∠OQ1M，
∴△Q1OM∽△CBO
∴Q1的坐标为（3，0）过点O作OB的垂线交抛物线的对称轴于Q2，
∴∠Q2OM=∠BCO=90°
∵对称轴平行于y轴，
∴∠Q2MO=∠BOC，
∴△Q2MO∽△BOC
∵∠Q2OM=∠COA=90°
∴∠Q1OQ2=∠COB
∵Q1O=CO=3，∠Q2Q1O=∠BCO，
∴△Q2Q1O≌△BCO，
∴Q1Q2=CB=4，
∵点Q2位于第四象限，
∴Q2的坐标为（3，-4）
因此符合条件的点有两个，分别是Q1（3，0）、Q2（3，-4）