某日有雾的清晨,一艘质量为m=500t的轮船,从某码头由静止起航做直线运动,并保持发动机的输出功率等于额定功率不变,经t0=10min后,达到最大行驶速度vm=20m/s,雾也恰好散开,此时船长突然发现航线正前方S=480m处,有一只拖网渔船以v=5m/s的速度沿垂直航线方向匀速运动,且此时渔船船头恰好位于轮船的航线上,轮船船长立即下令采取制动措施,附加了恒定的制动力F=1.0×105N,结果渔船的拖网越过轮船的航线时,轮船也恰好从该点通过,从而避免了事故的发生。已知渔船连同拖网总长度L=200m(不考虑拖网渔船的宽度),假定水对船阻力的大小恒定不变,求:
(1)轮船减速时的加速度a;
(2)轮船的额定功率P;
(3)发现渔船时,轮船离开码头的距离。

解:(1)渔船通过的时间t=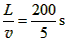 =40s
=40s
由运动学公式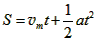 ,
,
得到 =-0.4m/s2
=-0.4m/s2
(2)轮船做减速运动时,牛顿第二定律:-( F+ Ff) =ma
解得Ff=1.0×105N
最大速度行驶时,牵引力F=Ff= 1.0×105N,
功率P=Fvm= Ff
vm=1.0×105×20W=2.0×106W
(3)由动能定理得
解得S1= m=1.1×104
m=1.1×104
