问题
计算题
有A、B两辆车，在平直的公路上同向同地出发，A车做初速度为30m/s ，加速度为6m/s2的匀减速运动，B车做初速度为6m/s，加速度为2m/s2的匀加速直线运动，则，A、B两车何时相距最远，相距的最远距离是多少，B车追上A车时两车的位移？
答案
解：A车做匀减速直线运动，A车的速度公式vA=v1+a1t
A车的位移sA=v1t+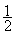
a1t2 ,
B车做匀加速直线运动，B车的速度公式vB=v2+a2t
B车的位移sB=v2t+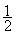
a2t2
当两车速度相等，即vA=vB时，两车相距最远，解得t=3s
此时两车相距S=sA-sB=36m
若两车相遇则有sA=SB解得：t=6s，而对A车根据vA=v1+a1t
得A车停止运动的时间t=5s<6S,即A车停止运动后，B车才追上A车，所以A车的总位移为B车运动的总位移。将t=5s，带入sA=v1t+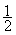
a1t2，解得位移为：sA=SB=75m。