问题
问答题
如图所示,一束带负电荷e,质量为m的电子流,平行于x轴以速度v0射入第Ⅰ象限区域,为使这束电子能经过x轴上的b点,可在第Ⅰ象限某区域加一个正y方向的 匀强电场,场强大小为E,其范围沿y方向无限大,沿x轴方向宽度为s,已知oa=L,ob=2s.求电场右边界线跟b点的距离.
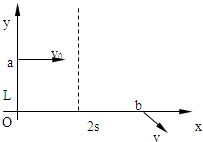
答案
电子在电场中的轨迹是一条抛物线,而且一定经过b点,要考虑b点可能在电场中,也可能在电场外,所以会出现几种可能的情况,无论电子在电场中
沿-y方向的偏移量总可以用下式表示:y0=1 2
t2①qE m
第一种情况:如果恰好y0=L,则电场的右边界恰好在b点,
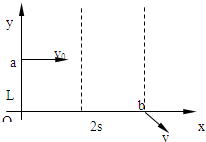
左边界在ob的中点,t=
,将①式 的y0以L代入,L=s v0 1 2 qE m s2 v02
所以电场右边界线跟b点的距离为零.
第二种情况:如果b点在电场内电场右边界跑到b点的右方,
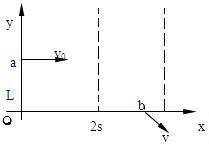
则s>x,L<y0,t=
<x v0
,因为L=s v0 1 2 qE m
=s2 v02 1 2 qE m x2 v02
所以x=v02ml qE
结论:电场的左边界位于b点左方v0
处,右边界距b点为向右(s-v02ml qE
)处2ml qE
第三种情况:整个电场都在b的左方,
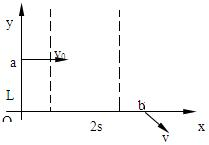
一定有y0=1 2 qE m
<L,s2 v02
注意到
=L-y0 x
=vy v0 qE m
,s v02
可求得x=
(L-y0)=mv02 qEs
(L-mv02 qEs
)qEs 2mv02
可见电场的右边界在b点左方
(L-m v 20 qEs
)远处qEs 2m v 20
答:电场右边界线跟b点的距离可能值是:零或b点左方v0
处或b点左方2ml qE
(L-m v 20 qEs
)远处.qEs 2m v 20
