问题
问答题
倾角θ=30°,质量M=5kg的粗糙斜面位于水平地面上.质量m=2kg的木块置于斜顶端,从静止开始匀加速下滑,经t=2s到达底端,运动路程L=4m,在此过程中斜面保持静止(sin37°=0.6,cos37°=0.8,g取10m/s2).求:
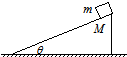
(1)地面对斜面的摩擦力大小与方向;
(2)地面对斜面的支持力大小;
(3)通过计算证明木块在此过程中满足动能定理.
答案
(1)木块做加速运动L=
at2,所以:a=1 2
=2m/s2,2L t2
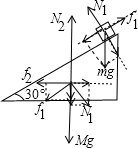
对木块由牛顿定律mgsinθ-f1=ma
解得:f1=mgsinθ-ma=8N,N1=mgcosθ=16N,
对斜面由共点力平衡,地对斜面的摩擦力f2=N1sinθ-f1cosθ=3.2N,方向水平向左.
(2)地面对斜面的支持力N2=Mg+N1cosθ+f1sinθ=67.6N,
(3)木块在下滑过程中,沿斜面方向合力及该力做的功为
F=mgsinθ-f1=4N,W=FL=16J.
木块末速度及动能增量v=at=4m/s,△Ek=
mv2=16J,1 2
由此可知下滑过程中W=△Ek,动能定理成立.
答:(1)地面对斜面的摩擦力大小为3.2N,方向水平向左;(2)地面对斜面的支持力大小为67.6N;(3)下滑过程中W=△Ek,动能定理成立.
