问题
解答题
求函数y=9x-3x+1的最小值．
答案
令3x=t，则y=t2-t+1（t＞0），∴y=(t-
)2+1 2
（t＞0）．3 4
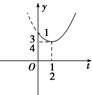
如图所示，可知y≥
，即当t=3 4
时，ymin=1 2
．3 4
∴函数的最小值是
．3 4
搜题请搜索小程序“爱下问搜题”
求函数y=9x-3x+1的最小值．
令3x=t，则y=t2-t+1（t＞0），∴y=(t-
)2+1 2
（t＞0）．3 4
如图所示，可知y≥
，即当t=3 4
时，ymin=1 2
．3 4
∴函数的最小值是
．3 4