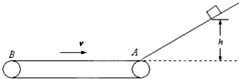
如图所示,足够高的光滑斜面倾角为30°,其下端有一很短的光滑圆弧与传送带的上表面紧靠,传送带做顺时针方向传动.一个质量为m的物体(物体可以视为质点),从高h=0.8m处由静止沿斜面下滑,物体与传送带间的动摩擦因数为0.4,物体向左滑行离开A点的最远距离为传送带上AB间距的四分之一,取g=10m/s2,试求:
(1)物体由静止沿斜面下滑到斜面末端需时间t;
(2)传送带上AB间距离LAB;
(3)对于传送带不同的传动速度v,若将物体轻轻放在传送带左端的B点,试求物体沿斜面上滑的最大高度.
(1)根据牛顿第二定律得,a=
=gsin30°=5m/s2.mgsin30° m
根据
=h sin30°
at2,解得t=0.8s.1 2
(2)物体滑上传送带的速度v=at=4m/s.
物体滑上传送带做匀减速直线运动,则加速度的大小a′=μg=4m/s2.
则物体匀减速直线运动到速度为零的位移x=
=v2 2a′
m=2m.16 8
所以LAB=4x=8m.
(3)物体放上传送带若一直做匀加速直线运动,则末速度v=
=2a′LAB
m/s=8m/s2×4×8
若传送带的速度v>8m/s,则物体一直做匀加速直线运动,到达A点的速度为8m/s.
则
=h sin30°
,解得h=3.2m.v2 2a
若传送带的速度v<8m/s,则物体先做匀加速直线运动再做匀速直线运动,则到达A点的速度为v.
则
=h sin30°
,解得h=v2 2a
.v2 20
可知上升的最大高度为3.2m.
答:(1)物体由静止沿斜面下滑到斜面末端需时间为0.8s.
(2)传送带上AB间距离为8m.
(3)物体沿斜面上滑的最大高度为3.2m.
