问题
选择题
下列命题,其中真命题的个数是( )
①有一个锐角相等的两个直角三角形相似;②两个等边三角形一定相似;
③有一个内角是100°的两个等腰三角形相似;④任意两个矩形一定相似.
A.1个
B.2个
C.3个
D.4个
答案
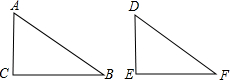
∵∠A=∠D,∠C=∠E=90°,
∴△ACB∽△DEF,∴①是真命题;
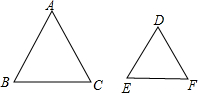
∵△ABC和△DEF都是等边三角形,
∴∠B=∠E=60°,∠C=∠F=60°,
∴△ABC∽△DEF,∴②是真命题;
根据三角形的内角和定理:等于100°的角只能是顶角,即△ABC和△DEF的顶角∠A=∠D=100°,
∵AB=AC,DE=DF,
∴∠B=∠C=
(180°-∠A)=40°,∠E=∠F=1 2
(180°-∠D)=40°,1 2
∴∠B=∠E,
∵∠A=∠D,
∴△ABC∽△DEF,∴③是真命题;
∵正方形也是矩形,
∴当一个是正方形,而另一个是一般矩形时,两个矩形就不相似,∴④是假命题;
故选C.