问题
解答题
在四边形ABCD中,E是AD上一点,且BE∥CD,AB∥CE,△ABE的面积记为S1,△BEC的面积记为S2,△DEC的面积记为S3。
(1)试判断△ABE与△ECD是否相似,并说明理由;
(2)当S1=6,S3=3时,求S2的值。
(3)猜想S1,S2,S3之间的等量关系。
答案
解:(1)∵BE∥CD,
∴∠BEC=∠DCE,
∵AB∥CE,
∴∠BEC=∠ABE,∠A=∠DEC,
∴∠DCE=∠ABE,
∴△ABE∽△ECD。
(2)∵△ABE∽△ECD,S1=6,S3=3
所以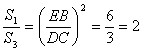
所以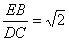
又因为BE∥CD,
所以△BEC和△DEC边BE和DC上的高相等
所以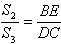
即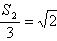
所以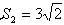 。
。
(3)结论: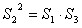
BE∥CD,
所以△BEC和△DEC边BE和DC上的高相等
所以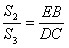
AB∥CE可得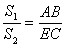
因为△ABE∽△ECD
所以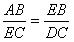
所以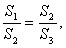
即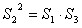 。
。
