问题
解答题
在矩形ABCD中,已知AB=a,BC=b,P是边CD上异于点C、D的任意一点。
(1)若a=2b,当点P在什么位置时,△APB与△BCP相似(不必证明)?
(2)若a≠2b,①判断以AB为直径的圆与直线CD的位置关系,并说明理由;②是否存在点P,使以A、B、P为顶点的三角形与以A、D、P为顶点的三角形相似(不必证明)?
答案
解:(1)当点P为CD中点时,△APB∽△BCP;
(2)当a>2b时:
①以AB为直径的圆与直线CD相交,
理由是:∵a>2b,
∴b<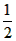 a,
a,
∴AB的中点(圆心)到CD的距离b大于半径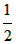 a,
a,
∴CD与圆相交;
②当点P为CD与圆的交点时,△ABP∽△PAD,即存在点P(两个),使以A、B、P为顶点的三角形与以A、D、P为顶点的三角形相似;
当a<2b时:
①以AB为直径的圆与直线CD相离;
理由是:∵a<2b,
∴b>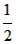 a,
a,
∴AB的中点(圆心)到CD的距离b大于半径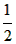 a,
a,
∴CD与圆相离;
②由①可知,点P始终在圆外,△ABP始终为锐角三角形,
∴不存在点P,使得以A、B、P为顶点的三角形与以A、D、P为顶点的三角形相似。
