问题
填空题
已知命题p:对一切x∈[0,1],k•4x-k•2x+1+6(k-5)≠0,若命题p是假命题,则实数k的取值范围是______.
答案
由已知,命题非p:对一切x∈[0,1],k•4x-k•2x+1+6(k-5)═0在x∈[0,1]有解是真命题,
构造函数f(x)=k•4x-k•2x+1+6(k-5),则f(x)=k•4x-k•2x+1+6(k-5),在区间[0,1]有零点
∴f(0)×f(1)≤0,即5(k-6)×6(k-5)≤0,
∴5≤k≤6,即实数k的取值范围是[5,6]
故应填[5,6]

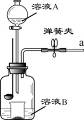 (1)检查装置气密性后,燃烧匙中放入少量的白磷,小烧杯内放入适量的碳酸钠粉末,组装好装置。打开弹簧夹,将溶液A缓慢加入到小烧杯内,溶液A是______,一段时间后,______(填写后续实验步骤和现象),关闭分液漏斗的活塞、弹簧夹,然后用凸透镜加热白磷,观察到白磷不燃烧,该实验过程的目的是______。
(1)检查装置气密性后,燃烧匙中放入少量的白磷,小烧杯内放入适量的碳酸钠粉末,组装好装置。打开弹簧夹,将溶液A缓慢加入到小烧杯内,溶液A是______,一段时间后,______(填写后续实验步骤和现象),关闭分液漏斗的活塞、弹簧夹,然后用凸透镜加热白磷,观察到白磷不燃烧,该实验过程的目的是______。