问题
选择题
在数列{an}中,a1=1,an+1-an=n(n∈N*),则a100的值为( )
A.5 050
B.5 051
C.4 950
D.4 951
答案
答案:D
由于a2-a1=1,a3-a2=2,a4-a3=3,…,an-an-1=n-1,
以上各式相加得
an-a1=1+2+3+…+(n-1)=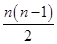 ,
,
即an=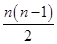 +1,
+1,
所以a100=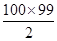 +1=4 951,故选D.
+1=4 951,故选D.
在数列{an}中,a1=1,an+1-an=n(n∈N*),则a100的值为( )
A.5 050
B.5 051
C.4 950
D.4 951
答案:D
由于a2-a1=1,a3-a2=2,a4-a3=3,…,an-an-1=n-1,
以上各式相加得
an-a1=1+2+3+…+(n-1)=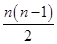 ,
,
即an=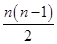 +1,
+1,
所以a100=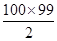 +1=4 951,故选D.
+1=4 951,故选D.