问题
解答题
在等差数列{an}中,a2+a7=-23,a3+a8=-29.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an+bn}是首项为1,公比为c的等比数列,求数列{bn}的前n项和Sn.
答案
(Ⅰ)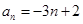 ;(Ⅱ)当c=1时,Sn=
;(Ⅱ)当c=1时,Sn=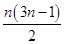 +n=
+n=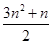 ;当c≠1时,Sn=
;当c≠1时,Sn=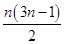 +
+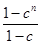 .
.
题目分析:(Ⅰ)根据等差数列的通项公式,列出方程组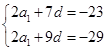 ,解得
,解得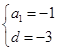 ,从而写出通项公式为
,从而写出通项公式为 ;(Ⅱ)根据题目条件,写出
;(Ⅱ)根据题目条件,写出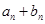 的通项公式为an+bn=cn-1,代入
的通项公式为an+bn=cn-1,代入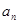 ,得出
,得出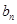 的通项公式bn=3n-2+cn-1,可知
的通项公式bn=3n-2+cn-1,可知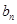 是由等差数列和等比数列组成,则根据分组求和得出
是由等差数列和等比数列组成,则根据分组求和得出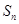 ,但注意等比数列的公比
,但注意等比数列的公比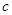 ,讨论当
,讨论当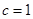 ,和当
,和当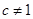 两种情况.
两种情况.
试题解析:(Ⅰ)设等差数列{an}的公差为d,则
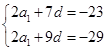 解得
解得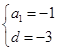
∴数列{an}的通项公式为an=-3n+2.
(Ⅱ)∵数列{an+bn}是首项为1,公比为c的等比数列,
∴an+bn=cn-1,即-3n+2+bn=cn-1,∴bn=3n-2+cn-1.
∴Sn=[1+4+7+…+(3n-2)]+(1+c+c2+…+cn-1)
=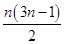 +(1+c+c2+…+cn-1).
+(1+c+c2+…+cn-1).
当c=1时,Sn=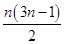 +n=
+n=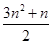 ;当c≠1时,Sn=
;当c≠1时,Sn=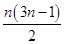 +
+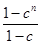 .
.
