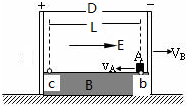
如图所示,绝缘长方体B置于水平面上,两端固定一对间距D=1m的平行带电极板,极板间形成方向水平向右的匀强电场,两板间电压为U=2×103V.长方体B的上表面光滑,下表面与水平面的动摩擦因数μ=0.05(设最大静摩擦力与滑动摩擦力相同).B与极板的总质量mB=1.0kg.带正电量q=6×10-4C的小滑块A的质量mA=0.60kg.假设A所带的电荷量不影响极板间的电场分布.t=0时刻,小滑块A从B表面上的b点以相对地面的速度vA=1.6m/s向左运动,同时B(连同极板)以相对地面的速度vB=0.40m/s向右运动.
(l)两板间的电场强度E为多大?
(2)B刚开始运动时的加速度大小为多少?
(3)若滑块A相对于长方体B最远能到达c点,则b、c的距离L应为多少?
(1)两板间的电场强度为E=
=2×103V/mU D
(2)小滑块受到的电场力为F=qE=1.2N,
根据牛顿第三定律,长方体B所受到的电场力为F′=F=1.2N
B刚开始运动时,受到电场力与摩擦力作用,摩擦力F1=μ(mA+mB)g=0.8N,
B刚开始运动时的加速度大小为aB=
=2m/s2F′+Ff mB
(3)设B从开始匀减速到零的时间为t1,则有t1=
=0.2svB aB
sB1=
=0.04mvBt1 2
t1时刻A的速度vA1=vA-aAt1=1.2m/s>0
A的位移sA1=
=0.28m(vA+vA1)t1 2
此t1时间内A相对B运动的位移s1=sA1+sB1=0.32m
w1=-f•sB1=-0.032J
t1后,由于F′>f,B开始向右作匀加速运动,A继续作匀减速运动,当它们速度相等时A、B相距最远,
设此过程运动时间为t2,它们速度为v,则有对A:速度v=vA1-aAt2
对B:加速度aB1=
=0.4m/s2F′-f mB
速度v=aB1t2解得:v=0.2m/s t=0.5s
t2时间内A运动的位移sA2=
=0.35m(v+vA1)t2 2
B运动的位移sB2=
=0.05mvt2 2
t2内A相对B的位移s2=sA2-sB2=0.30m摩擦力对B做功为w1=-f•sB2=-0.04J
A最远到达b点a、b的距离为L=s1+s2=0.62m
答:(l)两板间的电场强度E为2×103V/m;
(2)B刚开始运动时的加速度大小为2m/s2;
(3)若滑块A相对于长方体B最远能到达c点,则b、c的距离L应为0.62m.
