问题
解答题
数列{an}中,S1=1,S2=2,S n+1﹣3Sn+2S n﹣1=0(n≥2),求数列的通项an以及数列前n项和Sn.
答案
解:∵数列{an}中,S1=1,S2=2,S n+1﹣3Sn+2S n﹣1=0(n≥2),
∴a1=1,a2=1,
且 S n+1﹣S n﹣2 S n+2 S n﹣1=0(n∈N*且n≥2),
即(S n+1﹣Sn)﹣2(Sn﹣S n﹣1)=0(n∈N*且n≥2),
∴a n+1=2an(n∈N*且n≥2),
故数列{an}从第2项起是以2为公比的等比数列.
数列{an}的通项公式为 an=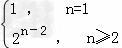 .
.
当n=1时,Sn =1.
当n≥2时,Sn =1+ =2 n﹣1.
=2 n﹣1.
综上可得 Sn =2 n﹣1.
