问题
问答题
如图所示，固定的光滑水平绝缘轨道与竖直放置的光滑绝缘的圆形轨道平滑连接，圆形轨道处于水平向右的匀强电场中，圆形轨道的最低点有A、B、C、D四个小球，已知
，A球带正电，电量为q，其余小球均不带电．电场强度
，圆形轨道半径为R=0.2m．小球C、D与处于原长的轻弹簧2连接，小球A、B中间压缩一轻且短的弹簧，轻弹簧与A、B均不连接，由静止释放A、B后，A恰能做完整的圆周运动．B被弹开后与C小球碰撞且粘连在一起，设碰撞时间极短． g取10m/s2，求：
(1) A球刚离开弹簧时，速度为多少
(2) 弹簧2最大弹性势能．
答案
（1）
（2）EP m=
(1) 根据带电小球A恰能做完整的圆周运动，因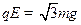
，则小球能通过复合场中的最高点P（如图）设经过轨道上的P点的速度为v，由小球A的重力和电场力的合力提供向心力有：
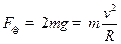…………①
在圆周轨道的最低点弹簧将B、A两球向左、右弹开，设弹开时A、B两球的速度大小分别为vA、vB，由动量守恒有：
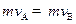，即
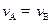…………②
小球A从圆周轨道的最低点运动到P的过程中，由动能定理有：
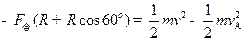…③
由①②③求得：
(2)设BC碰后速度为v1, B与C碰撞动量守恒
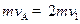得v1=2m/S …④
BC整体减速,D球加速,当两者速度相等时设为v2,弹簧最短,弹性势能最大
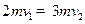得v2=
m/S ……⑤
EP m= ……⑥