问题
单项选择题
已知方程x2-4x+a=0有两个实根,其中一根小于3,另一根大于3,a的取值范围是()。
A.a≤3
B.a>3
C.a<3
D.0<a<3
答案
参考答案:C
解析:
方法一 依题意:△=(-4)2-4a>0, 得a<4.不妨设 x1<3,x2>3则 _x1-3<0,x2-3>0从而 (x1-3)(x2-3)<0即 x1x2-3(x1+x2)+9<0依韦达定理,得 a-3·4+9<0所以a<3,选(C).如图1一3所示.
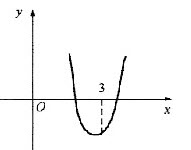
方法二 设f(x)=x2-4x+a依题意:必有 f(3)<0即 32-4×3+a<0所以a<3.
