问题
解答题
在数列{an}中，a1=2，an+1=4an-3n+1，n∈N*，
（1）证明：数列{an-n}是等比数列；
（2）求数列{an}的前n项和Sn。
答案
（1）证明：由题设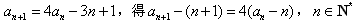
，，
又
，
所以，数列{an-n}是首项为1，且公比为4的等比数列。
（2）解：由（1）可知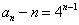
，
于是数列{an}的通项公式为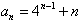
，
所以数列{an}的前n项和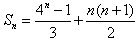
。
搜题请搜索小程序“爱下问搜题”
在数列{an}中，a1=2，an+1=4an-3n+1，n∈N*，
（1）证明：数列{an-n}是等比数列；
（2）求数列{an}的前n项和Sn。
（1）证明：由题设，，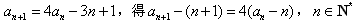
又，
所以，数列{an-n}是首项为1，且公比为4的等比数列。
（2）解：由（1）可知，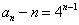
于是数列{an}的通项公式为，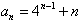
所以数列{an}的前n项和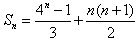。