某公园举办雕塑展览吸引着四方宾客.旅游人数x与人均消费t(元)的关系如下:x=
(1)若游客客源充足,那么当天接待游客多少人时,公园的旅游收入最多? (2)若公园每天运营成本为5万元(不含工作人员的工资),还要上缴占旅游收入20%的税收,其余自负盈亏.目前公园的工作人员维持在40人.要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费) |
(1)设当天的旅游收入为L,那么L=xt,得L=
;-12t2+1600t (10≤t≤50,t∈N) -6t2+1300t (50<t≤200,t∈N)
当10≤t≤50时,L=-12t2+1600t≤-12×502+1600×50=50000(元),
当50<t≤200时,L=-6t2+1300t=-6(t-
)2+325 3
,211250 3
∵t∈N,∴当t=108元时,Lmax=70416(元),此时x=652(人);
故当天接待旅游人数为652人时旅游收入最多,最多收入为70416元.
(2)要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营,即每天的旅游收入上缴税收后
不低于54000元,因(-12t2+1600t)max=50000≤54000,(10≤t≤50),显然不满足条件;
由(-6t2+1300t)×80%≥54000,得3t2-650t+33750≤0,(50<t≤200),∴87≤t≤130;
此时旅游人数x满足:520≤x≤778,故每天的游客人数应控制在520人到778人之间.

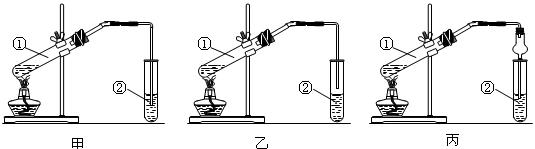 请从甲、乙两位同学设计的装置中选择一种作为实验室制取乙酸乙酯的装置,应选择的装置是 (选填“甲”或“乙”)。丙同学设计了丙装置,用球形干燥管代替玻璃管,除了起到冷凝作用外,另一重要作用是 。
请从甲、乙两位同学设计的装置中选择一种作为实验室制取乙酸乙酯的装置,应选择的装置是 (选填“甲”或“乙”)。丙同学设计了丙装置,用球形干燥管代替玻璃管,除了起到冷凝作用外,另一重要作用是 。