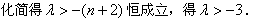第四部分:写作(共两节 满分 35分)
第一节:语篇填空(共10小题;每小题1分,满分10分)
Ladies and gentlemen:
Welcome to our class and to our evening party. Here we
feel greatly _____ (荣幸) to have a good chance to be with you. 76.________
First of all, let me say a few words a____ our class. There are 77.________
45 students in our class. 32 of us are boys, ___ the rest are 78.________
girls. Most of us are studying English, and we_____(通常)spend 79.________
much time on it. We often read English______(杂志),newspapers 80.________
and watch English programs on TV in our spare time. We are ________(决心) 81. _______
to learn English well so ____ to have a better job in the future. 82.________
In our program tonight, t___ are cross talks, short plays, group singing, 83.________
popular songs and so on. I hope you will enjoy them and ____ a good time. 84.________
And of c______ your participation would be appreciated. 85.________
Thank you.
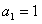 及
及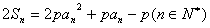 ,
,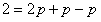 ,∴p=1。
,∴p=1。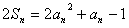 , ①
, ① ,(n≥2,n∈N*), ②
,(n≥2,n∈N*), ②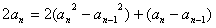 ,
,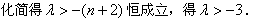 ,
,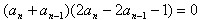 ,
,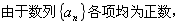
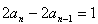 ,即
,即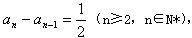
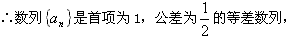
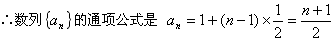 。
。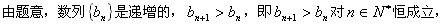
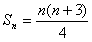 ,
,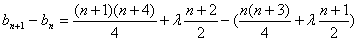 >0恒成立,
>0恒成立,