问题
解答题
已知{bn}是公比大于1的等比数列，b1，b3是函数f(x)=x2-5x+4的两个零点，
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）若数列{an}满足an=log2bn+b+2，且a1+a2+a3+…+am≤63，求m的最大值。
答案
解：（Ⅰ）因为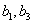
是函数
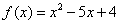的两个零点，
所以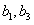
是方程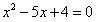
的两根，故有
，
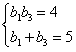因为公比大于1，所以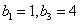
，则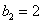
，
所以，等比数列{bn}的公比为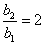
，
。
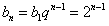（Ⅱ）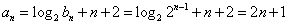
，
所以，数列{an}是首项为3，公差为2的等差数列，
故有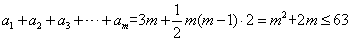
，
即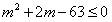
，解得-9≤m≤7，
所以m的最大值是7。