问题
解答题
已知{an}是等差数列,{bn}是公比为q的等比数列,a1=b1,a2=b2≠a1,记Sn为数列{bn}的前n项和,
(1)若bk=am(m,k是大于2的正整数),求证:Sk-1=(m-1)a1;
(2)若b3=ai(i是某一正整数),求证:q是整数,且数列{bn}中每一项都是数列{an}中的项;
(3)是否存在这样的正数q,使等比数列{bn}中有三项成等差数列?若存在,写出一个q的值,并加以说明;若不存在,请说明理由。
答案
| 解:设 |
(1)因为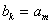 |
所以 |
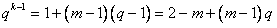 |
所以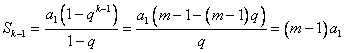 。 。 |
(2)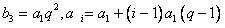 |
由 |
所以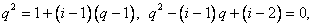 |
解得 或 或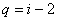 |
但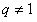 |
所以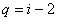 |
因为i是正整数,
所以 是整数,即q是整数,
是整数,即q是整数,
设数列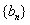 中任意一项为
中任意一项为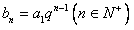
设数列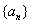 中某一项
中某一项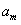
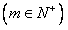 =
=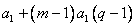
现在只要证明存在正整数m,使得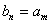 ,即在方程
,即在方程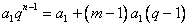 m中有正整数解即可,
m中有正整数解即可,
所以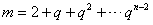
若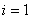 ,则
,则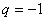
那么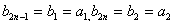
当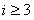 时,因为
时,因为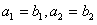
只要考虑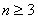 的情况
的情况
因为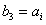
所以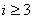
因此q是正整数,
所以m是正整数,
因此数列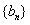 中任意一项为
中任意一项为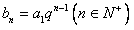 与数列
与数列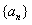 的第
的第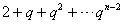 项相等,
项相等,
从而结论成立。
(3)设数列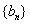 中有三项
中有三项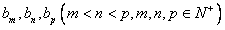 成等差数列,则有
成等差数列,则有
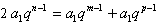
设
所以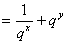
令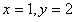
则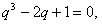
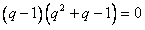
∵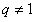
所以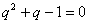
所以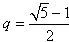 (舍去负值)
(舍去负值)
即存在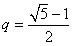 使得
使得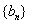 中有三项
中有三项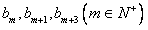 成等差数列。
成等差数列。
