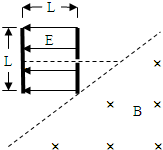
如图所示,竖直放置的正对平行金属板长L,板间距离也为L,两板间有场强为E的匀强电场(电场仅限于两板之间),右极板的下端刚好处在一有界匀强磁场的边界(虚线所示)上,该边界与水平成45°夹角,边界线以石有垂直纸面向里的匀强磁场.一质量为m、电量为e的电子在左侧金属板的中点从静止开始,在电场力作用下加速向右运动,穿过右极板中心小孔后,进入匀强磁场.
求:(1)从电子开始运动到进入匀强磁场所需的时间;
(2)匀强磁场的磁感应强度B应满足什么条件,才能保证电子从磁场出来后,还能穿越平行金属板间的电场区域.
(1)电子在电场中做匀加速运动,设离开电场时速度为v,所用时间为t1,根据牛顿第二定律及运动学公式得:
a=eE m
L=
a1 2 t 21
v=at1
电子从离开电场到进入磁场做匀速直线运动,所用时间为t2,则:
=vt2L 2
设从电子开始运动到进入云强磁场所需的时间为t,则:
t=t1+t2=5 2 mL 2eE
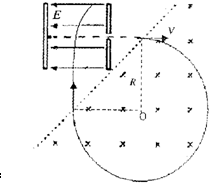
(2)电子在磁场中做圆周运动,经3/4周从磁场射出时,速度应沿竖直方向,在电场中做类平抛运动.设电子穿越电场所需时间为t3,偏转距离为x,则
L=vt3
x=
a1 2 t 23
为保证电子从磁场射出后能进入电场并能从电场中射出,电子在磁场中运动的半径R应满足:
+x≤R≤L 2
+LL 2
由 m
=qvBv2 R
得 R=mv BR
由以上公式可得:2 3
≤B≤2mE eL 4 3 2mE eL
答::(1)从电子开始运动到进入匀强磁场所需的时间为5 2
.mL 2eE
(2)匀强磁场的磁感应强度B应满足2 3
≤B≤2mE eL 4 3
,才能保证电子从磁场出来后,还能穿越平行金属板间的电场区域.2mE eL
