问题
问答题
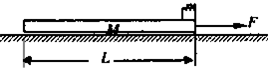
质量为m=1.0kg的小滑块(可视为质点)放在质量为M=3.0kg的长木板的右端,木板上表面光滑,木板与地面之间的动摩擦因数为μ=0.2,木板长L=1.0m.开始时两者都处于静止状态,现对木板施加水平向右的恒力F=l2N,如图所示.为使小滑块不掉下木板,试求:(g取l0m/s2)
(1)用水平恒力F作用的最长时间;
(2)水平恒力F做功的最大值.
答案
(1)撤力前后木板先加速后减速,设加速过程的位移为x1,加速度为a1,加速运动的时间为t1;
减速过程的位移为x2,加速度为a2,减速运动的时间为t2.由牛顿第二定律得:
撤力前:F-μ(m+M)g=Ma1,解得:a1=
m/s2,4 3
撤力后:μ(m+M)g=Ma2 ,
解得:a2=
m/s2x1=8 3
a11 2
,x2=t 21
a21 2 t 22
为使木块不从木板上掉下,应满足:x1+x2≤L,
又a1t1=a2t2,由以上各式可解得:t1≤1s,
即作用的最长时间为1s.
(2)木板在拉力F作用下的最大位移:x1=
a11 2
=t 21
×1 2
×1m=4 3
m,2 3
所以F做功的最大值:W=Fx1=12×
J=8J;2 3
答:(1)用水平恒力F作用的最长时间是1s;
(2)水平恒力F做功的最大值是8J.
