问题
解答题
(10分)为了了解某学校餐厅的饭菜质量问题,采用分层抽样的方法从高一、高二、高三三个年级中抽取6个班进行调查,已知高一、高二、高三年级分别有18、12、6个班.
①求从高一、高二、高三年级分别抽取的班级个数;
②若从抽取的6个班中随机抽取2个进行调查结果的对比,试列出所有可能的抽取结果,并且计算抽取的2个班中至少有1个来自高一年级的概率.
答案
①从高一、高二、高三年级分别抽取的班级个数3,2,1;②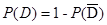 =1-
=1-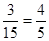
题目分析:(1)由题意知总体个数是6+8+12,要抽取的个数是6,做出每个个体被抽到的概率,分别用三个年级的数目乘以概率,得到每一个年级要抽取的班数.
(2)由题意知本题是一个古典概型,从6个班中随机地抽取2个班共有C62个等可能的结果,其中这两个班都来自高二、三年级的共有C32个结果,这两个班来自至少有一个来自高一年级的共有C62- C32个结果,得到概率.
解:①从高一、高二、高三年级分别抽取的班级个数3,2,1;
②抽取的6个班中,高一三个班记为: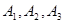 ;高二两个班记为:
;高二两个班记为: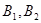 ;高三一个班记为:
;高三一个班记为: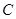 ,则抽取2个班的所有可能结果为:
,则抽取2个班的所有可能结果为:
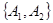 ,
,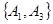 ,
,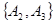 ,
,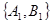 ,
,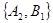 ,
,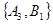 ,
, ,
,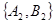 ,
,
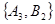 ,
,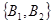 ,
,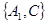 ,
, ,
,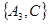 ,
,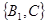 ,
,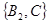 , 共15种.
, 共15种.
抽取的2个班中至少有1个来自高一年级,记为事件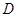 ,则事件
,则事件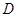 的对立事件
的对立事件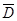 包括:
包括: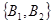 ,
,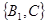 ,
,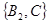 ,共3种,故
,共3种,故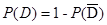 =1-
=1-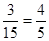
点评:解决该试题的关键是理解分层抽样的等比例性质,以及古典概型概率中试验的总体数和事件发生个基本事件数。
