问题
解答题
设等差数列{an}满足a3=5，a10=﹣9．
（Ⅰ）求{an}的通项公式；
（Ⅱ）求{an}的前n项和Sn及使得Sn最大的序号n的值．
答案
解：（1）由am=a1+（n﹣1）d及a3=5，a10=﹣9
得a1+9d=﹣9，a1+2d=5
解得d=﹣2，a1=9，
数列{am}的通项公式为an=11﹣2n
（2）由（1）知Sn=na1+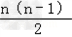
d=10n﹣n2．
因为Sn=﹣（n﹣5）2+25．
所以n=5时，Sn取得最大值．
、H2O、Mn2+、H2O2、H+。已知该反应中H2O2只发生了如下过程：H2O2→O2↑。