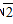如图所示,质量M=1kg的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1,在木板的左端放置一个质量m=1kg、大小可以忽略的铁块,铁块与木板间的动摩擦因数μ2=0.4,取g=10m/s2,试求:
(1)若木板长L=1m,在铁块上加一个水平向右的恒力F=8N,经过多长时间铁块运动到木板的右端?
(2)在铁块上加一个水平向右多大范围的力时,铁块和木板间存在相对运动?
(3)若在铁块上的右端施加一个大小从零开始连续增加的水平向右的力F,通过分析和计算,写出铁块受到木板的摩擦力f2与拉力F大小的关系式.(设木板足够长)
(1)铁块的加速度大小为:a1=
=4m/s2F-μ2mg m
木板的加速度大小为:a2=
=2m/s2μ2mg-μ1(M+m)g M
设经过时间t铁块运动到木板的右端,则有:
a1t2-1 2
a2t2=L1 2
解得:t=1s
(2)设F=F1时,A、B恰保持相对静止,此时系统的加速度为:a=a2=2m/s2
以系统为研究对象,根据牛顿第二定律有:F1-μ1(m+M)g=(m+M)a
解得:F1=6N
所以,当6N<F时,铁块和木板间存在相对运动
(3)①当F≤μ1(mg+Mg)=2N时,A、B相对静止且对地静止,f2=F
②当2N<F≤6N时,M、m相对静止,系统向右做匀加速运动,其加速度为:
a=
=F-μ1(M+m)g M+m
-1,F 2
以M为研究对象,根据牛顿第二定律有:f2-μ1(M+m)g=Ma,
解得:f2=
+1 F 2
③当F>6N,A、B发生相对运动,f2=μ2mg=4N
答:(1)若木板长L=1m,在铁块上加一个水平向右的恒力F=8N,经过1s铁块运动到木板的右端;
(2)在铁块上加一个水平向右大于6N的力时,铁块和木板间存在相对运动;
(3)当F≤2N时,f2=F;当2N<F≤6N时,:f2=
+1;当F>6N时,f2=4N.F 2