问题
解答题
为了让学生了解更多“奥运会”知识，某中学举行了一次“奥运知识竞赛”，共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成并有局部污损的频率分布表，解答下列问题：
(1)若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为000，001，002，…799， 试写出第二组第一位学生的编号； (2)填充频率分布表的空格(将答案直接填在表格内) ，并作出频率分布直方图； (3)若成绩在85.5~95.5分的学生为二等奖，问参赛学生中获得二等奖的约多少人？ |
答案
(1)编号为016 ；（2）如下图所示 ；（3）约256人.
题目分析：（1）800人抽取50人，则分成50组，每组16人，所以第二组的第一位学生的编号为016号.
（2）根据公式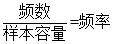
计算即可.频率分布直方图如下图所示.作图时注意横坐标为分数，纵坐标为
.
（3）在被抽到的学生中获二奖的人数是9+7=16人，占样本的比例是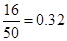
，即获二等奖的概率约为32%，所以获二等奖的人数估计为800×32%=256人.
试题解析：(1)编号为016；
(2)
| 分组 | 频数 | 频率 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 18 | 0.36 |
| 90.5~100.5 | 14 | 0.28 |
| 合计 | 50 | 1 |
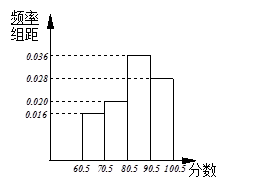
(3)在被抽到的学生中获二奖的人数是9+7=16人，占样本的比例是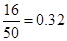，即获二等奖的概率约为32%，所以获二等奖的人数估计为800×32%=256人.