问题
问答题
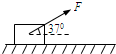
如图所示,质量m=2kg的物体原静止在水平地面上,物体与地面间的动摩擦因数μ=0.75,一个与水平方向成37°角斜向上、大小F=20N的力拉物体,使物体匀加速运动,2s后撤去拉力.求物体在地面上从静止开始总共运动多远才停下来?(sin37°=0.6,cos37°=0.8,g=10m/s2)
答案
开始时物体受重力、支持力、摩擦力、拉力作用.
竖直方向上 ΣFy=N+Fsin37°-mg=0…①
由①得 N=mg-Fsin37°…②
水平方向上 ΣFx=Fcos37°-μN…③
所以 Fcos37°-μ(mg-Fsin37°)=ma1
a1=
=Fcos37°-μ(mg-Fsin37°) m
=5m/s220×0.8-0.75×(2×10-20×0.6) 2
头2s物体的位移 S1=
a1t2=1 2
×5×22m=10m1 2
第2s末物体的速度 v=a1t=10m/s
拉力撤去后,摩擦力 f=μmg
设加速度大小为a2 a2=
=μg=7.5m/s2 f m
位移S2=
=0-v2 2a2
m=6.7m0-102 7.5×2
总位移S=S1+S2=16.7m
答:物体在地面上从静止开始总共运动16.7m.
