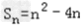问题
解答题
设递增等差数列{an}的前n项和为Sn，已知a3=1，a4是a3和a7的等比中项，
（I）求数列{an}的通项公式；
（II）求数列{an}的前n项和Sn．
答案
解：（I）在递增等差数列{an}中，设公差为d＞0，
∵
， ∴ 
，
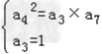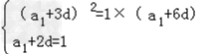解得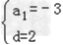
∴an=﹣3+（n﹣1）×2=2n﹣5．
（II）由（I）知，在等差数列中，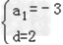
，
∴ 
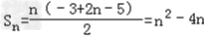
故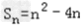 
搜题请搜索小程序“爱下问搜题”
设递增等差数列{an}的前n项和为Sn，已知a3=1，a4是a3和a7的等比中项，
（I）求数列{an}的通项公式；
（II）求数列{an}的前n项和Sn．
解：（I）在递增等差数列{an}中，设公差为d＞0，
∵ ， ∴ ，
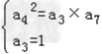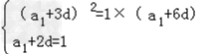解得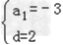
∴an=﹣3+（n﹣1）×2=2n﹣5．
（II）由（I）知，在等差数列中， ，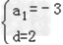
∴
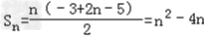
故