连结BD，证△BED≌△CFD和△AED≌△BFD，求得EF=5

分析：首先连接BD，由已知等腰直角三角形ABC，可推出BD⊥AC且BD=CD=AD，∠ABD=45°再由DE丄DF，可推出∠FDC=∠EDB，又等腰直角三角形ABC可得∠C=45°，所以△EDB≌△FDC，从而得出BE=FC=3，那么AB=7，则BC=7，BF=4，再根据勾股定理求出EF的长．

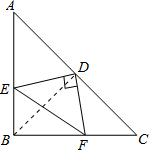
解：连接BD，

∵等腰直角三角形ABC中，D为AC边上中点，

∴BD⊥AC（三线合一），BD=CD=AD，∠ABD=45°，

∴∠C=45°，

∴∠ABD=∠C，

又∵DE丄DF，

∴∠FDC+∠BDF=∠EDB+∠BDF，

∴∠FDC=∠EDB，

在△EDB与△FDC中，

∵，

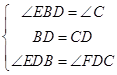∴△EDB≌△FDC（ASA），

∴BE=FC=3，

∴AB=7，则BC=7，

∴BF=4，

在Rt△EBF中，

EF²=BE²+BF²=3²+4²，

∴EF=5．

答：EF的长为5．