问题
解答题
已知{an}为等差数列，且a1+a3=8，a2+a4=12。
（1）求{an}的通项公式；
（2）记{an}的前n项和为Sn，若a1，ak，Sk+2成等比数列，求正整数k的值。
答案
解：（1）设等差数列{an}的公差等于d，
则由题意可得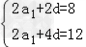
，解得 a1=2，d=2。
{an}的通项公式an=2+（n-1）2=2n。
（2） 由（1）可得{an}的前n项和为Sn =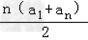
=n（n+1）
∵若a1，ak，Sk+2成等比数列，
∴
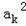=a1Sk+2 ，
∴4k2 =2（k+2）（k+3），k=6 或k=-1（舍去），
故k=6。