∵|a|=2，|b|=3，c的相反数是最小的正整数，

∴a=±2，b=±3，c=-1，

又∵ab＜0，

∴①a=-2，b=3，c=-1；②a=2，b=-3，c=-1，

（1）a-b-c=-2-3-（-1）=-2-3+1=-4，

或a-b-c=2-（-3）-（-1）=2+3+1=6；

（2）∵ab=-2×3=-6或ab=2×（-3）=-6，即ab=-6，

∴|a-b-c|+ab=4-6=-2，

或|a-b-c|+ab=6-6=0，

答：（1）a-b-c值为-4或6；（2）|a-b-c|+ab的值为-2或0．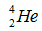