答案：C

专题：计算题．

分析：连接ED，根据BD和CE分别是两边上的中线，并且BD⊥CE，BD=4，CE=6，先求出S四边形BCDE=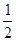BD?CE=12．然后利用DE是△ABC两边中点连线即可求得答案．解答：解：如图，连接ED，

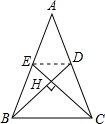
则S四边形BCDE=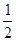DB?EH+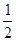BD?CH= 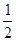DB（EH+CH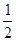）=BD?CE=12．

又∵CE是△ABC中点

∴S△ACE=S△BCE，

∵D为AC中点，

∴S△ADE=S△EDC，

∴S△ABC=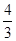 S四边形BCDE= 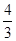×12=16．

故选C．

点评：此题考查学生对三角形面积的理解和掌握，解答此题的关键是连接ED，求出S四边形BCDE．